기하학을 정리하면서 내심 느끼는게 3D를 지금까지 정확하게 이해했다고 착각하고 있거나 또는 나는 충분히 알았는데 생각해보면 그 대상을 3D의 관점, 입체의 관점을 수학적으로 잘 설명할수 있는가? 라는것이다.
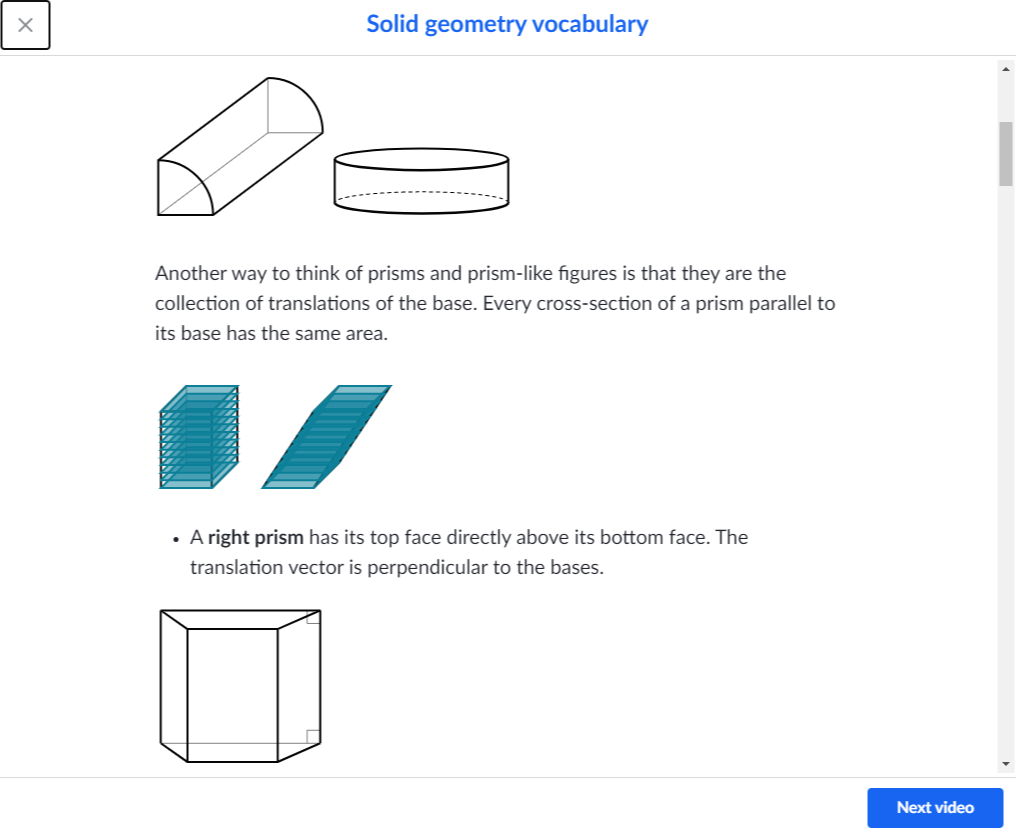
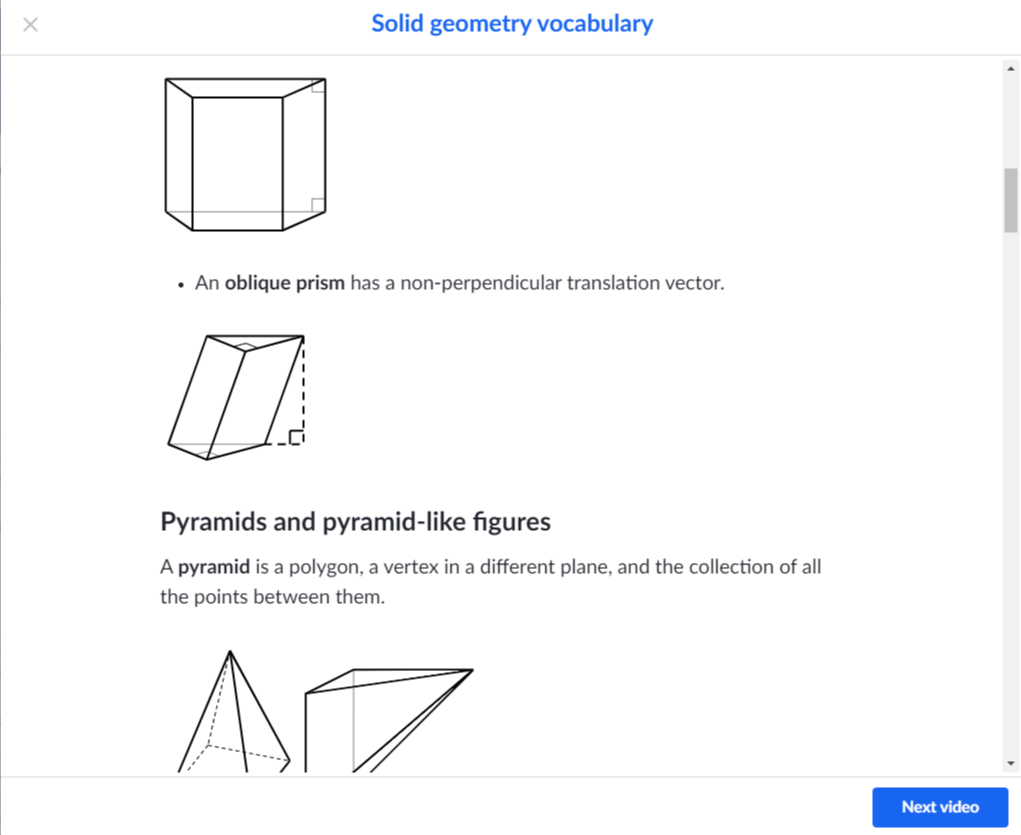
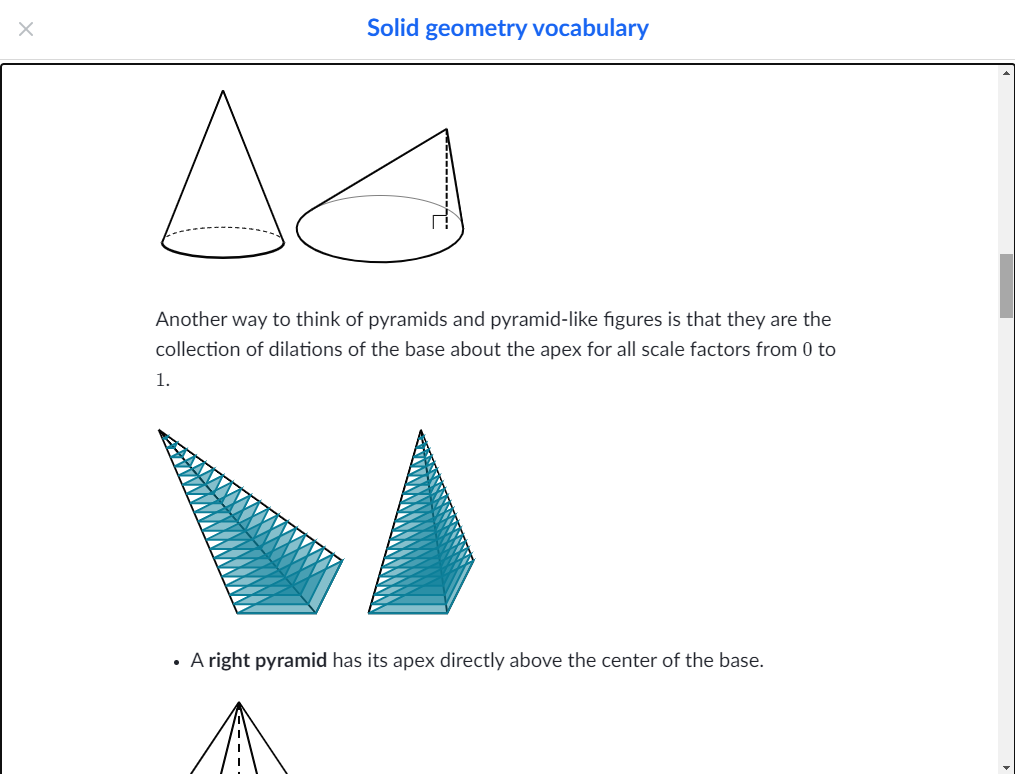
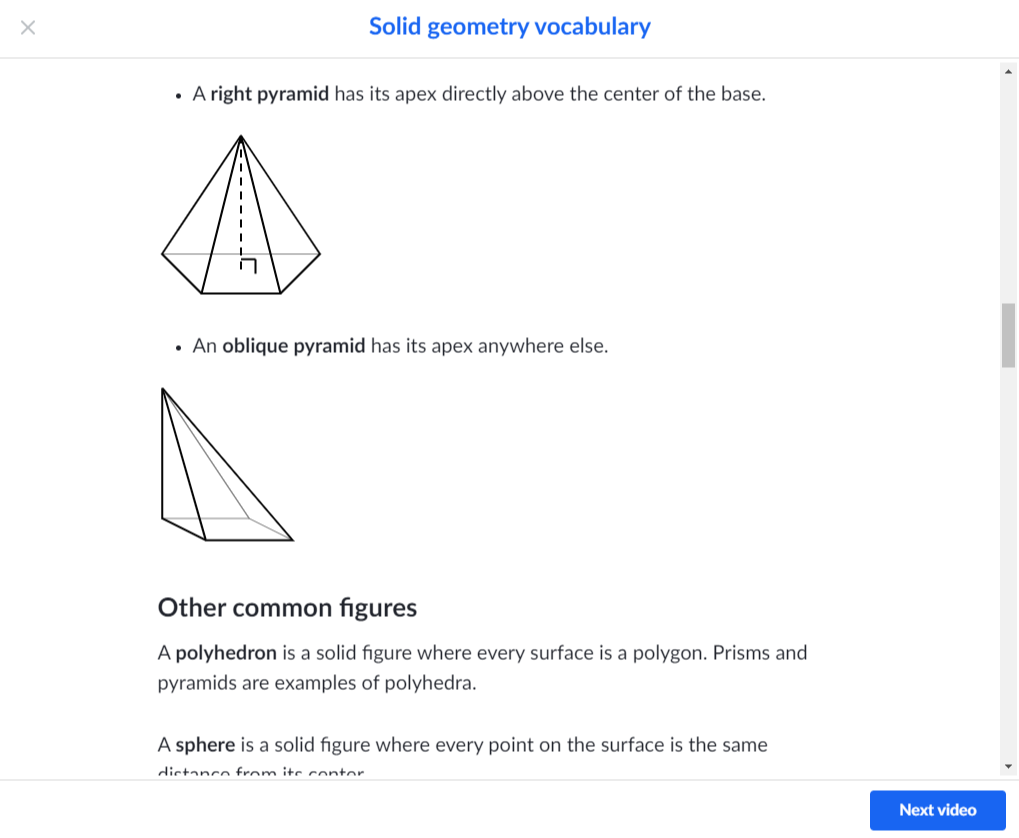
원뿔(a cone)과 원기둥 (cylinder) 각뿔과(pyramid) 각기둥(Prism)
2.그동안 기하학 형태를 Key, Value 값으로 이 그림은 원뿔이야, 이 그림은 원기둥이야 이런식으로 공부했던건지도 모른다. 그리고 대부분의 사람들도 그렇게 입체,사물, 오브젝트들을 인지하고 정확히 그게 왜 원기둥이고 왜 원뿔이고,
그것에 대해 어떠한 특징이 있는지 설명을 잘 못하고 그냥 그게 원뿔이잖아 그냥 그게 각뿔이잖아 라고 할 것이다.
(모든 사물에는 특징이 있다. 기하학은 기초적인 사물에 특징을 말하고 분석하는데 매우 중요한 학문이다.)
3.하지만 각각의 2D 도형과 3D 도형은 차이점과 공통점이 있고 그것이 이루어져있는 형태를 설명하고 증명 할수 있어야
3D를 제대로 이해했다고 할수 있다. 그저 마음 가는대로 외우는게 아니다.






'Mathematics > Geometry' 카테고리의 다른 글
| 기하학 정리 36번째(입체 기하학) (0) | 2021.02.16 |
|---|---|
| 기하학 정리 35번째 (입체 기하학,블렌더를 사용하며 정리) (0) | 2021.02.12 |
| 기하학정리 33번째 (원과 관련된 건설법) (0) | 2021.02.09 |
| 기하학정리 32번째(원의접선) (0) | 2021.02.09 |
| 기하학 정리 31번째(원주각,inscribed angle) (0) | 2021.02.09 |



