라디안을 기억하고 어떻게 응용할지 아직도 혼란이 오지만 천천히 공부해서 차근차근 정리하자면
응용 할수 있는날이 올것이다.
라디안의 개념은 어차피 전체 호의 길이의 일부분의 호는 전체 각도의 일부분의 각도 와 비가 항상 일정하다 라는
개념에서 나온다.
그리고 라디안은 라인/반지름 이렇게 해서 각도를 실수로 표현이 개념이다.


일단 라디안을 각도로 바꾸고 라디안을 다시 각도로 바꾸는 공식은 위와 같이
라디안 x 180/파이 -> 라디안을 각도로 바꾸는 공식
각도 * 파이/180 - > 각도를 라디안으로 바꾸는 공식
어려울 것 없이 확실한 것 부터 천천히 차근 차근 정리하자.

분명 호와 각도의 비는 항상 일정하다고 앞에서 서술했다 그렇다면
-파이 : 3 == 파이 : 180 이게 된다면 수학적으로
내항과 외항의 곱은 같으니까
잘 기억이 나지 않지만 어쨋든 외항을 분자로 내항을 분모로
번분수식으로 정리해서 답을 유추할수있다.
왜 이렇게 번분수식으로 정리할수있는지 근본적인 이유는 까먹었다.
-180파이 / 3파이 = -60

라디안의 개념은 각도를 실수로 표현하는데에 있고 360 degree ==2pi*r
세타라는 임의의 각도가 2radians를 나타낸다고 했을때 호의 길이는 반지름인 radius(r)의 두배인 2r 이다.
그것을 정확히 둘레의 길이를 구하는 분수식(호이든 각도이든 항상 분모는 2pi*r 또는 360)으로 정리한다면
호의길이
= 2r/(2pi*r)
= 1/pi
라디안 복습 과정

라디안은 다시 한번 말하지만 각도를 호의길이를 반지름과 연관지어 표시해 실수로 나타내는 개념이고(이렇게 하는 이유는 일부분의호를 전체호로 나눈 비와 일부분의 각도를 전체 각도로 나눈것의 비는 항상 일정하기 때문에)
구하는 공식은 호의길이(l)/ 반지름의 길이(r) 이므로 복잡하게 생각할것 없이 반지름 5를 0.5 라디안을 곱하면
2가 나온다 반대로 이것을 2/5로 하면 0.4가 나온다.
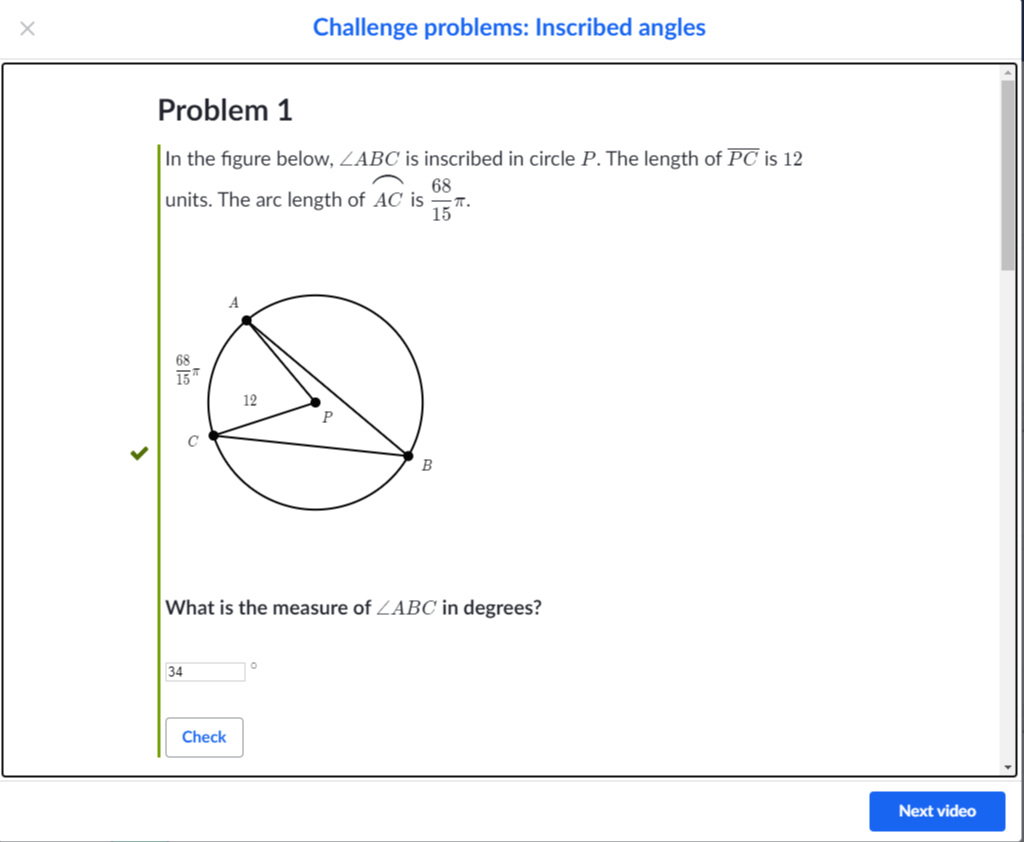
68/15 (pi) = 12 * 세타 = 호의길이
68/15(pi)*1/12 = 세타 = 라디안의 공식
17(pi)/45 (라디안) = 세타 = 각도를 라디안으로 바꾸는데 성공
17(pi)/45 * 180/파이 = 라디안을 각도로 바꾸는 공식
17/45 * 180 = 68
inscribed angle = 원주각은 34 degree
'Mathematics > Geometry' 카테고리의 다른 글
| 기하학정리 32번째(원의접선) (0) | 2021.02.09 |
|---|---|
| 기하학 정리 31번째(원주각,inscribed angle) (0) | 2021.02.09 |
| 기하학 정리29번째 (라디안) (0) | 2021.02.05 |
| 기하학 정리 28번째(원의호 그리고 호의 각도,호의길이) (0) | 2021.02.04 |
| 기하학 정리 27번째 (포물선과 직선 그리고 원) (0) | 2021.01.29 |




