dilatation :
transformation :
Transformation means something is changing,
it s transforming from one thing to another.
What would transformation mean in a mathmatical context?
quadrilateral
quadrilateral
quadrilateral
quadrilateral
quadrilateral
quadrilateral
Now all of the transformations that I have just showed you
1. translation 옮기는 것
2. rotation 회전하는것
3. reflection 대칭으로 반대쪽에 매칭 시키는 형태
these are called rigid transfotmations.
a rigid transformation is one in which lengths and angles
are preserved.
dilation is scale up and down.
================================================================
What is a rotation ?
In the figure below, one copy of the trapezoid is rotating around the point.
In geometry, rotations make thing turn in a cycle around
a definite cetner point. Notice that the distance of each rotated point
from the center remains the smae. Only the relative position changes.
회전을 할려면 항상 회전 중심 축이 있고
그 중심축으로 부터 끝지점 까지 선을 그은 다음
회전을 한 각도가 몇도 인지가 중요한 개념이 아닐까??
In the figure below, one copy of the octagon is rotated 22 degree
around the point.
Notice how the octagon's sides change direction, but the general shape
remains the same. Rotations don;t distort shapes(중요), they just whirl
them around. Furthermore, note that the vertex that is the center of the rotation
does not move at all.
Not the we have got a basic understanding of what rotations are, let's learn
how to use them in a more exact manner.
The angle of rotation
Every rotation is defined by two important parameters : the center of the rotation
we already went over that and the angle of the rotation.
The angle determines by how much we rotate the plane about the center.(중요)
For example, we can tell that A' is the result of rotation A bout P, but that ;s not
exact enough.
즉 회전을 정의할 때는 내가 앞서 말했다 시피 중심축과 중심축 에서 부터 시작해 A'
A의 끝점 까지의 선들의 회전이 중요한 것이다.
In order to define the measure of the rotation, we look at the angle that's created between the segments
ㅡ ㅡ
PA PA' 선분 사이의 이루는 각의 정도를 본다.
In order to define the measure of the rotation, we look at the angle that's created
between the segments PA and PA'
This way, we can say that A' is the result of rotation A by 45 degree about P.
아래는 좌표상 각도의 움직임이 시계방향, 시계반대방향으로 움직이는것에 대해 설명한 문서이다.
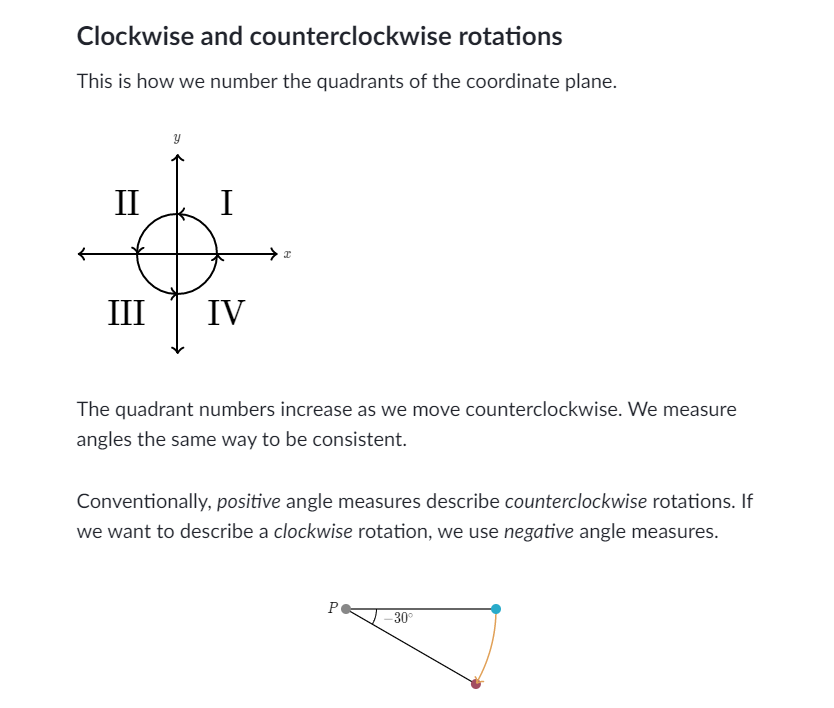
이미지 and 지식 출처 khan academy
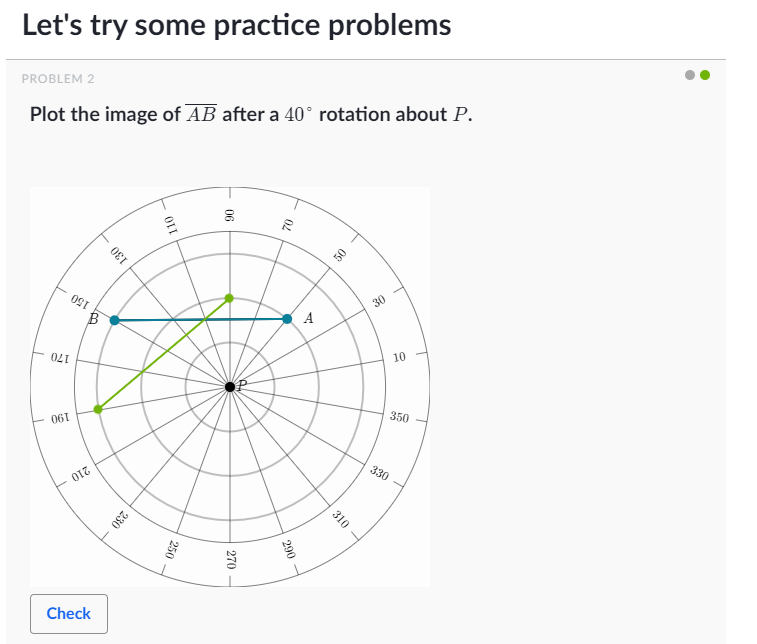
이미지 and 지식 출처 : khan academy
정말 매우 좋은 문제들이다. 나는 보통 3D 프로그램이나 그림을 그릴때 선의 회전을 대충
눈 대중으로 이정도면 길이가 똑같으면서 회전이 된거겠지 라고 무의식적으로 생각했을지 모르나
정말 회전을 정의하자고 한다면
1. 원을 이루는 중심점으로 부터 떨어진 거리가 같아야한다.
혹은 같은 원 라인의 속한 점이어야한다.
2. 그리고 한번 더 체크를 하기위해 회전한 물체는 크기나 길이의 변화가 없어야 한다.

공부하는데 다소 시간이 오래걸렸지만 그래도 테스트를 볼때 적어도 개념을 읽어서 그것을 인지할때
막힘이 없었다.
'Mathematics > Geometry' 카테고리의 다른 글
| 기하학 5번째 정리 (0) | 2020.12.11 |
|---|---|
| 기하학 정리 4번째 (1) | 2020.12.10 |
| 기하학 용어 정리 2번째 시간 (0) | 2020.12.10 |
| 기하학 영어 용어 정리 (0) | 2020.12.10 |
| 기하학 처음부터-1 (0) | 2020.12.06 |