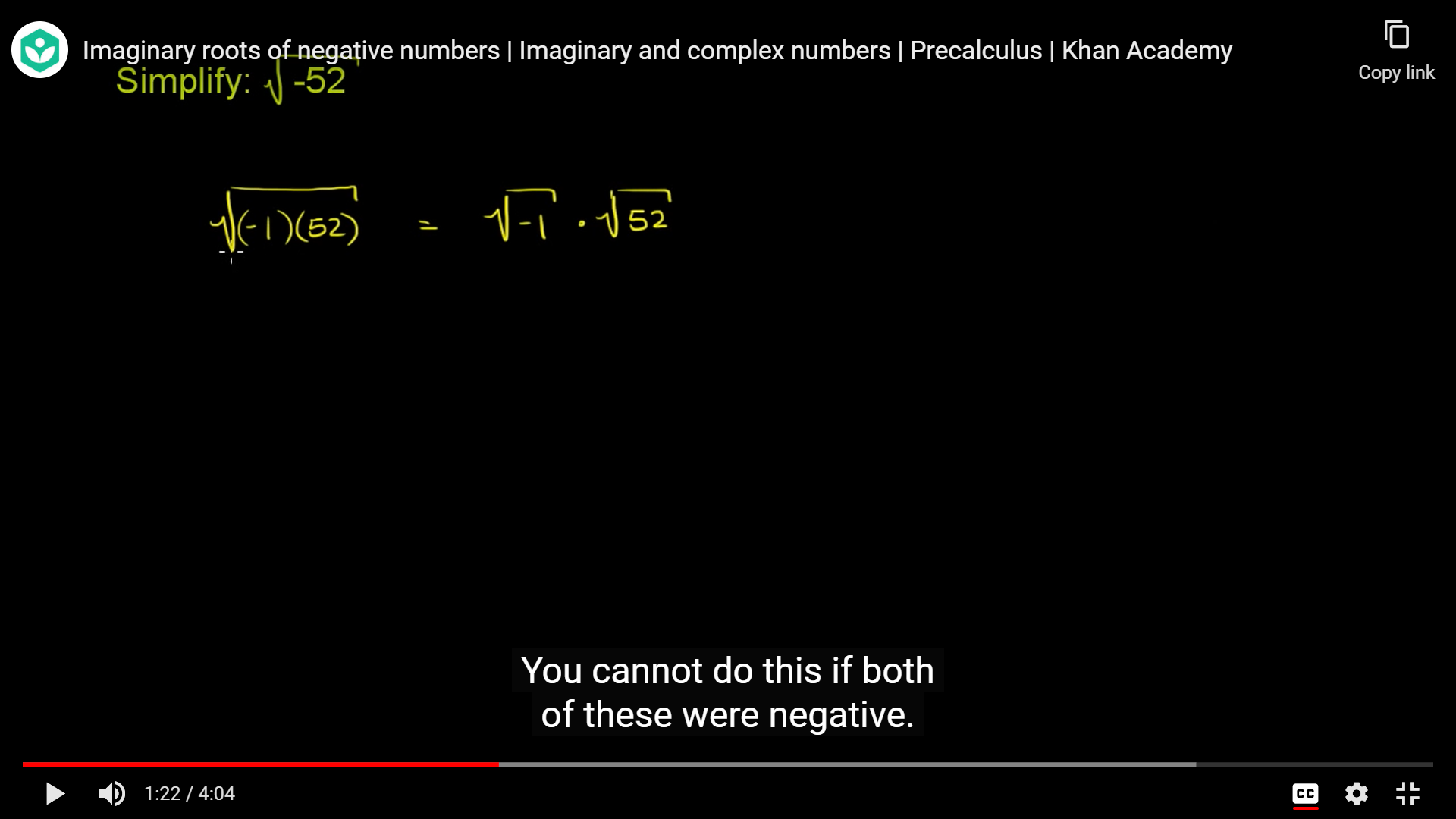

일단은 루트 -1은 복소수 i랑 같으니까 그걸 말하는것 같다.
아직 까지 켤레복 소수에 대해 특이사항은 i가 루트 -1 도 된다는거고
회전에서 이거를 어떻게 이용한다는건지는 감이 안온다.

솔직히 특이사항은 언급했다시피 이게 다이다 특별한거는 없다.

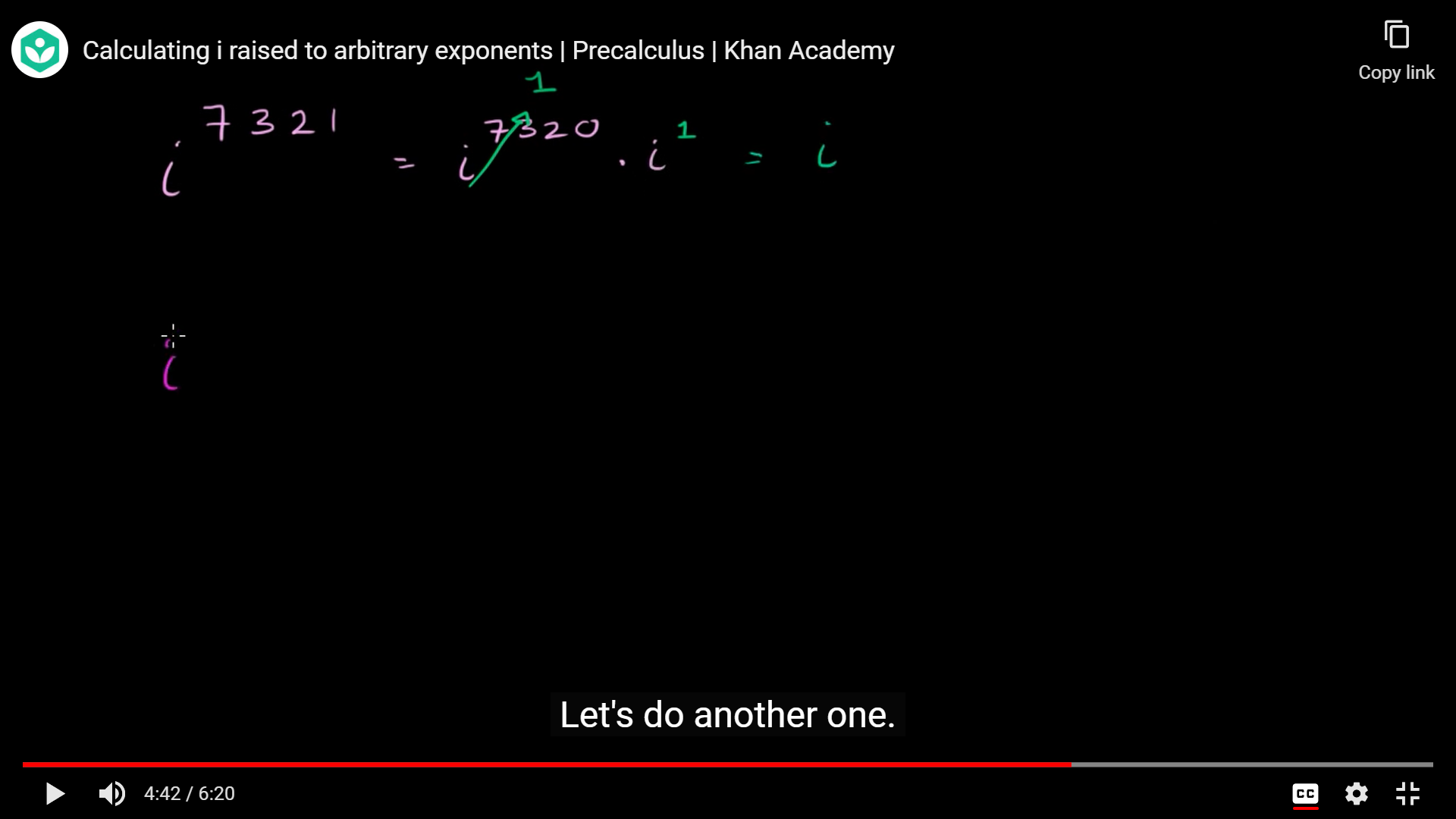
지수의 곱셈과 덧셈을 잘생각해야한다.



In your mathematical careers you might encounter people who say it is wrong to say



============================================================================
프로그래밍과 애니메이션에서 복소수를 활용을 어떻게 하는지에 대한 참고글
https://alleysark.tistory.com/entry/Mathematics-complex-number
[Mathematics] complex number
복소수(complex number)는 사원수(quaternion)를 이해하기 위해서 알아야할 개념이다. 사원수는 회전보간(interpolation)이나 카메라의 움직임을 설명할 때 빼놓을 수 없는 부분이기 때문에 사원수와 이의
alleysark.tistory.com
https://blog.naver.com/devdeepblue/220071358970
사원수(Quaternion) 이야기 (1)
0. 들어가기 앞서 Quaternion(사원수)는 컴퓨터 그래픽스 분야에서 꽤 자주 언급되는 이론입니다. 하지만 ...
blog.naver.com
지금은 그렇게 복잡하게 생각할것 없고 사원수에 대한 정의만 이해하면 된다.
사원수의 개념은 여기서부터 시작한다. 복소수의 2차원적 표현을 확장하여 허수부 하나 j를 더 추가하면, a + ib + jc 2차원적인 그래프 표현에 하나의 축을 추가하는것이므로 3차원의 표현이 된다.(와우!) 애석하게도 복소수를 통한 3차원 표현은 i^2 = -1과 같은 허수부의 연산에 있어서 i*j와 j*i를 풀지 못했다. 많은 연구가 있은 후 허수부 하나를 더 추가하여 a + ib + jc + kd 형태의 복소수 체계로 확장시켰고(즉 4차원의 표현) 오랜 기간에 걸쳐 허수부의 관계가 정립되었다.
출처: https://alleysark.tistory.com/211?category=543622 [앨리삵]
'Mathematics > Algebra2' 카테고리의 다른 글
| 대수학2 복소수 2021 04 17 (0) | 2021.04.17 |
|---|---|
| 대수학2 첫번째 시간(다항식) (0) | 2021.03.12 |


